Принципиальная сложность бытия, или О чем не рассказывают в школе

15 февраля – 458 лет со дня рождения великого ученого Галилео Галилея, заложившего, в том числе, фундамент классической механики. Он – один из основателей механицизма – метода познания и миропонимания, рассматривающего Вселенную как гигантский механизм, а сложные природные процессы – как комбинации простейших причин, главная из которых – механическое движение.

Из школьного курса физики мы помним три закона Ньютона, которые позволяют записать уравнения движения для механической системы. Люди нередко считают, что сложность и непредсказуемость появляются только в микромире, описываемом квантовой механикой.

Воспользуемся сегодняшней датой, чтобы обсудить то, о чем не говорится в школе на уроках физики, чтобы поговорить о том, что и в макромире все оказалось сложнее, чем полагал в свое время Галилей. И, как следствие, в динамической системе под названием «жизнь» не может быть простых, просчитанных, предсказуемых «траекторий движения».

Со времен основания классической механики было представление, что мы понимаем, как устроены уравнения, определяющие движение всех тел в природе. Классическая механика, созданная Ньютоном и Лапласом, утверждает принципиальную предсказуемость траекторий всех взаимодействующих тел: зная их начальные координаты и скорости, можно просчитать все, что случится с ними в будущем.

Небесная механика Ньютона-Лапласа объяснила все известные факты о движении планет и предсказала результаты новых астрономических наблюдений. Регулярное, хорошо предсказуемое движение демонстрируют маятник Фуко, законы баллистики.

Казалось, что все события в природе могут быть предсказаны, надо лишь знать начальные условия – координаты и скорости всех частиц системы, решить уравнения Ньютона, и узнать, что будет в будущем.

Но всегда ли это так? Всегда ли предсказуем мир классической физики? Ответ на этот вопрос был получен в конце XIX века, намного позже, чем была основана классическая механика. Это заслуга основателей общей теории устойчивости движения динамических систем Анри Пуанкаре и Александра Михайловича Ляпунова, заложивших также основы теории динамического хаоса.

Ответ таков: на большом интервале времени фактически непредсказуемы решения обычных уравнений Ньютона, если взаимодействует достаточно много тел сразу. Экспериментально его легко можно продемонстрировать, если взять не простой, а двойной маятник с двумя грузами, качающимися с разными частотами. Казалось бы – ничего особенного. Но это только до тех пор, пока колебания маятника малые.

При несильном колебании – предсказуемое движение. При сильном – динамика становится хаотичной, пропадают хорошо определенные траектории движения, конец маятника «заметает» целую область на плоскости, попадая время от времени в каждую доступную точку.

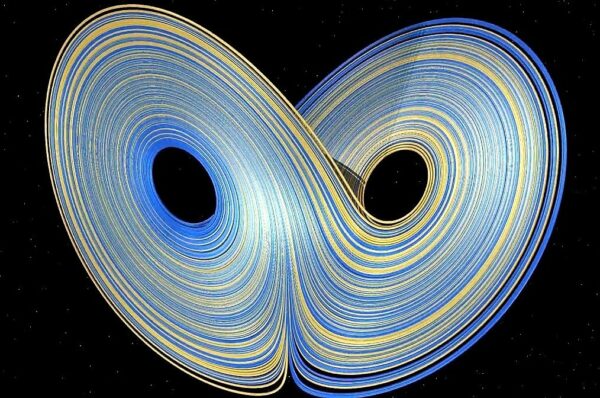
В таких случаях вместо простых регулярных траекторий движения («узел», «седло») появляются «странные аттракторы» (области притяжения траекторий). Странные аттракторы характеризуются неустойчивостью – если чуть поменяли начальные условия точек, то результаты их движения могут сильно отличаться, через некоторое время точки на траектории будут далеко друг от друга в непредсказуемых местах. Таким образом, малая начальная неточность приводит к ощутимым различиям.

Если у механической системы три и более степеней свободы, то появляется хаос, странный аттрактор. Например, у двойного маятника четыре степени свободы. Пример хаотического движения – турбулентность.

Большая система не всегда ведет себя хаотично – это зависит от ее параметров. Двойной маятник будет вести себя «очень прилично», если один из его грузов намного тяжелее другого. Хаос возникает, если массы грузов сравнимы. Причем, в случае близких масс малые колебания двойного маятника близки к гармоническим. А вот если мы раскачаем его сильно, с большой амплитудой, то получим непредсказуемый хаос.

Что же могут узнать физики о динамической системе, если ее траектории хаотичны? Как быть, если мы не можем решить уравнения механики, не можем понять, что будет с системой спустя какой-то, достаточно большой интервал времени?

Мы можем узнать, какова вероятность найти нашу систему в той или иной области ее фазового пространства. Можно вычислить ее статистические свойства. Там, где не работает классическая механика Ньютона-Лапласа, применяется статистическая механика Гиббса, Больцмана и Эйнштейна.

Мы теряем знание деталей, но можем описать среднее поведение системы, а также – насколько сильных отклонений от среднего стоит ожидать. То есть точное знание о положении точек системы принципиально недоступно никакому исчислению, но статистически, с точки зрения теории вероятностей, можно выяснить, насколько вероятна та или иная конфигурация динамической системы.

Вместо вопроса: «Какова траектория точки?» резонно спрашивать: «Какова вероятность найти точку в таком-то месте?»

Поскольку такие вероятности различны, и их можно вычислить, то существует распределение вероятностей. И физики в таких случаях уже решают не уравнения механики, а решают задачу написания распределения вероятностей того, что наша точка через длительный период времени попадет в ту или иную область. Также и в жизни – точные предсказания почти никогда не сбываются. Хотя многие люди склонны ожидать обратного.

Кажется, что если захотеть по-настоящему, приложить максимум усилий, можно предсказать и предусмотреть все и в экономике, и в политике, и в жизни общества, и в своей собственной жизни. А если что-то пойдет не так, то существует конкретный виновник, который проявил злой умысел. На этом основании пользуются популярностью различные теории заговоров.

Заговоры, конечно, случаются, но, на самом деле, хаос – вполне естественное состояние больших систем, и детальные предсказания, как правило, невозможны. И виновников чаще всего нет – «безобразия» происходят сами собой, естественным порядком. И заговоры оказываются недоразумениями.

А вот вероятность событий в разных сферах человеческой деятельности ученые могут рассчитать. И, исходя из такого прогноза, можно предпринять меры к тому, чтобы эту вероятность минимизировать, если вероятное событие негативное, или наоборот увеличить вероятность его осуществления.

Как сказал когда-то Альберт Эйнштейн: «Вы думаете, все так просто? Да, все просто. Но совсем не так».