Не бросайтесь тряпками!

Ситуация, когда ребенок жалуется родителям, что учитель его невзлюбил, знакома многим. «Характерами не сошлись», – вздыхает мама несчастного двоечника, а папа, не вдаваясь в детали, берется по старинке за ремень. Знали бы они, что во всем виноваты не ученик и не учитель, а таинственный кластер…

Пушкин, двойка!

Новгородский психолог Илья Каплунович, работая учителем в школе, заметил, что на уроках алгебры и геометрии разные ученики по-разному воспринимают материал. Одним нравится подробно расписывать решение задачи. Другие стремятся, проскочив промежуточные стадии, выдать ответ. Третьи не поймут, о чем идет речь в задаче, пока не нарисуют таблицу, схему.

Скоро Каплунович понял, что разное восприятие характерно для учеников и на уроках по другим предметам. И разделил всех на пять типов, или кластеров.

Первый кластер, по данной теории, – порядковый. Работа по правилу, образцу для таких детей любимое занятие. Второй кластер – проективный. Проективисты любят составлять проекты и планы, но терпеть не могут их детальную разработку. Они нетрадиционно смотрят на вещи, представляют объект с разных точек зрения. Третий – алгебраический, или композиционный, кластер. Алгебраисты быстро схватывают новое, устанавливают связи между фактами, но небрежны и могут допустить элементарную ошибку в вычислениях. Четвертая подструктура мышления – метрическая. Метристы любят измерять и подсчитывать. Это люди, для которых не алгебра поверена гармонией, а наоборот. Для них мир – это набор чисел. И наконец, человек с пятой подструктурой, топологической, не пропускает деталей или этапов, тщателен, часто медлителен, ему необходимо определить, что представляет собой предмет и каковы его связи с другими предметами.

– Проблема в том, – считает Илья Каплунович, – что новый материал учитель обычно объясняет согласно своему природному кластеру. Так, учитель-тополог будет рассказывать слишком подробно и скучно для ученика-алгебраиста. Тот уже все понял, у него свои идеи возникли, он тянет руку, а дотошный учитель его игнорирует и даже сердится.

История изобилует массой случаев, когда гении оказывались в числе неуспевающих. Например, известно, что Александр Сергеевич Пушкин получал в лицее двойки по математике. Объяснить это можно. Даже самый беглый анализ стихов поэта показывает, что ведущей у него была топологическая подструктура мышления:

Татьяна прыг в другие сени,
С крыльца на двор, и прямо в сад,
Летит, летит: взглянуть назад
Не смеет; мигом обежала
Куртины, мостики, лужок,
Аллею к озеру, лесок…

И таких топологических стихов Пушкина можно привести множество. Тогда несложно предположить, что тополога Сашу Пушкина на уроках математики заставляли решать числовые, метрические задачи, и тут он пасовал.

Другой пример. Гениальный французский математик Эварист Галуа дважды проваливался на экзаменах в политехническую школу, потому что давал правильные ответы без решения. Экзаменатор (очевидно, тополог) требовал подробного описания и не верил, что абитуриент способен совершать столь сложные преобразования в уме. Галуа же это мог в силу ведущей в его мышлении алгебраической подструктуры. В результате раздраженный вопросами Галуа… бросил в экзаменатора тряпку.

Добавим варенья!

Теорию кластеров применяют на практике учителя, например, из школы №33 Великого Новгорода, школы №8 города Старая Русса, образовательных учреждений Нижнего Новгорода, Иванова. Приведем фрагмент урока Марины Ильиной, педагога начальных классов новгородской гимназии «Квант». «Развернутый угол» – на такой теме урока математики, пожалуй, не развернешься. Но Марина Юрьевна считает по-другому.

– Скучных тем не бывает! Конечно, если я, алгебраист по своему типу кластера, буду объяснять урок всем ученикам одинаково, не все меня поймут, – рассуждает педагог. – Когда алгебраисты уже подхватили мою идею, проективисты и топологи витают в облаках. Что же делать? Я бы привела такое сравнение. Не все любят манную кашу. Но она полезна! Поэтому я в «манную кашу» знаний подмешаю «варенье» – применяю способ мышления, аналогичный природному кластеру ученика.

Вспомнив с детьми уже известные типы углов, Марина Юрьевна нарисовала на доске развернутый угол и предложила определить, что это за геометрическая фигура.

– Уж точно не угол! – заявили ученики из быстро думающего кластера алгебраистов.

Педагог, ведущий занятие по стандартной программе, вероятно, настоял бы на своем и объяснил учащимся: это угол, и он называется развернутым. Но цель учителя-экспериментатора в том, чтобы развивать мышление детей.

– Докажите свое мнение, – предложила Марина Юрьевна.

– Это не угол. Это прямая, посередине которой стоит точка, – включились в беседу дотошные топологи.

– А угол имеет вершину и два луча, выходящих из вершины, – сообщил кто-то из метристов, назубок помнящих определения.

– А здесь есть вершина? – спросила учительница.

– Есть. И есть два луча. Значит, это угол?! – в озадаченной тишине наконец воскликнул ученик-проективист, для которого ломать устоявшиеся понятия – любимое дело…

Так, без всякой (как им казалось) помощи учителя ученики открыли новый тип угла. Осталось подобрать название. Посыпались варианты: «Очень прямой! Развернутый! Тупее тупого!» Учительница заметила, что все они правы, но в математике уже выбрано одно из прозвучавших определений – развернутый угол.

В Женеве и в Париже…

…известна теория Ильи Каплуновича. В Великий Новгород приезжали узнать о ней педагоги из Норвегии, Франции, Германии, Голландии. Илья Яковлевич объездил с лекциями всю Россию – от Калининграда до Владивостока, был в странах ближнего и дальнего зарубежья. Интересно, что его теория востребована не только в педагогике, но и в бизнесе. Она может быть применена при создании любого рода команды, считает ученый. Вот типичный пример: на должность своего заместителя руководитель, как правило, назначает человека, с которым ему комфортно сосуществовать. Зачастую это представитель того же кластера, к которому принадлежит сам шеф. Но это неверное решение! Руководитель должен создать команду из представителей разных типов кластеров, чтобы одни могли подавать идеи, другие – детально их разрабатывать, третьи – реализовывать и т. д.

Чтобы определить свой тип кластера, пройдите небольшой тест. Назовите лишние цифры в ряду:

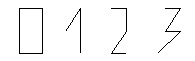
Сравните свой ответ со следующими. Лишние цифры:

– 0, так как она единственно замкнутая;

– 1 и 2, так как они не похожи на буквы;

– 1, так как в ее начертании нет параллельных отрезков;

– 1, так как состоит из двух отрезков, а другие из четырех;

– 1, так как остальные можно преобразовать друг в друга.

Какой из вариантов верный? Каплунович считает, в каждом есть свой резон. А вычленение особенностей изучаемых объектов зависит от того, какая из подструктур мышления у человека ведущая.

С помощью первой подструктуры – топологической – человек оперирует такими характеристиками, как непрерывность, компактность, связность, замкнутость образа и операции над ним.

Вторая, проективная, подструктура позволяет распознавать, создавать, представлять, оперировать объектами и ориентироваться среди них с любой точки отсчета, устанавливать соответствие между объектом и его проекциями.

Опираясь на третью, порядковую, подструктуру мышления, удается вычленять свойства и устанавливать отношения по размеру, расстоянию, форме, положению в пространстве.

Четвертая, метрическая, подструктура заточена на количественные преобразования, позволяет пересчитывать, измерять величины длин, углов, расстояний.

С помощью пятой, композиционной (алгебраической), подструктуры человек оперирует законами композиции, устанавливает обратимость преобразований, свертывает их, выполняет в любой последовательности, заменяет несколько операций одной.

Дети и кластеры

Каплунович рассказывает о примерах работы с кластерами:

– Дети, отдававшие в начальной школе предпочтение математике, в пятом классе вдруг потеряли интерес к этому предмету и воспылали любовью к русскому языку. Почему? Оказывается, учительница русского языка непроизвольно сформировала у ребят свою ведущую подструктуру. У преподавателя же математики она была иной. Как только последний перестроил по нашей рекомендации методику и стал общаться адекватно ведущей подструктуре подавляющего большинства учеников, ситуация нормализовалась. Очевидно, задача педагога – развивать мышление детей так, чтобы не ломать ведущую структуру, а максимально использовать ее, то есть сделать обучение гуманизированным.

Как развивать разные типы мышления у детей? Топологическое мышление отвечает за связь и единство в логических операциях. Начинать работу над его развитием можно к 3 годам. На помощь придут простейшие задания: «найди отличия между картинками», «что лишнее?», «найди сходство», «объедини предметы в группы». Порядковое мышление отвечает за последовательность логических операций, вырабатывает алгоритм действий и схем. Эта форма мышления встречается чаще других, потому что именно ей учат в школе. Порядковое мышление начинает развитие вслед за топологическим, то есть в 3-4 года. Соответствующие игры: счет на примере ступенек, пальчиков, игрушек. Детей старшего возраста учим формам и сравнению размеров геометрических фигур, их объединению. Метрическое мышление развивается следующим. Его главное свойство – просчет действий наперед. Игры для развития: шахматы, шашки, домино, лото.

Алгебраическое мышление отвечает за структурирование информации, новые комбинации. Характерно для конструкторов и инженеров. Игры на развитие: электронный конструктор, танграм, пазлы, сложить картинку из палочек или геометрических фигур. Проективное мышление дает умение смотреть на задачу с разных сторон, находить нестандартные пути решения, быть лидером, быстро оценить ситуацию и сделать вывод. Игры на развитие: составить план комнаты или дома, нестандартные задачи на логику или абстракцию.

В той или иной мере пять типов мышления есть у каждого из нас. Обычно ведущим является один тип, однако нужно стараться развивать все остальные. Причем для успешного развития, советует Каплунович, нужно найти тип мышления, развитый меньше других, и уделить ему больше внимания.

В заключение порадуемся за новгородского ученого: его работа «Каузально-генетическое формирование кластеров мышления» недавно была включена в официальный реестр новых научных направлений, в раздел «Психологические науки». На практике, к сожалению, теории развивающего обучения в российских школах не получают широкого распространения из-за общей нацеленности последних на оценки и результаты экзаменов. А учителя-энтузиасты, работающие в этом направлении, не удостаиваются поощрения.

Светлана ПОТАПОВА, Новгородская область, фото автора