Не секрет, что в 7-8‑х классах детей как будто подменяют: в подростковом возрасте с ними становится трудно общаться даже родителям, не говоря уже о попытках чему-то научить или подготовить к ВПР. В этом учебном году вдвойне «повезло» – проверочные работы мы будем писать весной уже второй раз.
У каждого учителя свои секреты работы с детьми в этот трудный для всех период, да и дети все разные. Важно помочь им распределить свое время, спланировать подготовку с учетом слабых мест в знаниях по предмету и последовательно повторить весь материал, необходимый для успешного прохождения проверочных работ. Именно поэтому выбор пособий издательства «Экзамен» стал моим небольшим секретом, которым я с удовольствием делюсь.
Некоторые задания, несмотря на внешнюю простоту записи, вызывают затруднения у ребят. Например, в 7‑м классе мы много работаем с упрощением выражений, но в учебнике почти нет таких заданий (см. рис. 1).
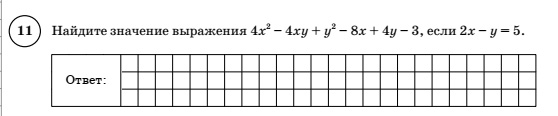
Обычно значения переменных даны отдельно, поэтому ребята затрудняются сразу решить это задание. Однако если увидеть в первых трех слагаемых квадрат разности, той самой, которая равна пяти, а в 4‑м и 5‑м слагаемых вынести за скобки минус 4, то получится:
(2x – y)2 – 4(2x – y) – 3 = 25 – 20 – 3 = 2
Задание №10 тоже непривычно для семиклассников (см. рис. 2).

Радость от новой встречи с Фалесом (на геометрии мы изучали теорему его же имени) будет недолгой: во второй части задачи именованные величины, с которыми нужно обращаться аккуратно, чтобы не получить несуразный ответ.
7,53 х 0,6 = 4,518 млрд кв. км.
Удивительно, но факт: мы все вполне поместимся на территории Стамбула! Тем не менее решение задачи предусматривает обоснование и расчеты, чего ребята делать не очень любят. Но в задачах с интересным сюжетом и расчеты становятся не такими скучными.
Если в ВПР для 7‑го класса заданий всего шестнадцать, то в 8‑м классе их уже 19, причем задания становятся достаточно серьезными. Эта работа – фактически демоверсия экзамена в 9‑м классе, например, задания по геометрии – 12, 13 и 14 – фактически часть экзаменационной работы: здесь и геометрия на листе в клетку, и решение треугольника, и определение верных утверждений. Кроме того, задание 17 готовит ребят к решению второй части экзамена с развернутым ответом.
Например, задание из варианта 5 (см. рис. 3).

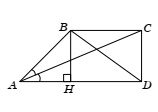
Рис. 3. ВПР. 8‑й класс. 25 вариантов. Вариант 5. Задание 17
Если ребята сразу не вспомнят, что биссектриса угла трапеции отсекает равнобедренный треугольник, то докажем это: углы CAD и BCA равны как накрест лежащие, то есть в треугольнике АВС углы ВАС и ВСА равны, то есть он равнобедренный с основанием АС. Значит,
![]() .
.
На чертеже к задаче есть маленькая подсказка: опустить высоту ВН. Так как угол А равен 45 градусам, то треугольник АВН – прямоугольный и равнобедренный с известной гипотенузой, тогда катеты равны 6 см.
Наконец, из прямоугольного треугольника ВСD по теореме Пифагора найдем:
BD2 = BC2 + CD2 = 72+36 = 108;
![]()
Решая такую задачу, ребята волей-неволей повторяют почти весь пройденный материал по геометрии!
Почему же мы выбираем именно эти пособия? Во-первых, авторы книг – это разработчики реальных КИМов к ВПР, их фамилии известны в самых широких кругах в системе образования. Во-вторых, сами пособия получили положительную оценку Федерального института оценки качества образования.
Удобно и проверять работы учеников: ко всем вариантам есть ответы, а к заданиям с развернутым решением и вариант решения, хотя, как известно, способов может быть несколько. Ключи к вариантам, впрочем, легко вынимаются, если книга используется для проверки знаний в школе, а могут быть оставлены для самопроверки подготовленных ребят, которые могут успевать больше остальных.
Юлия КАПАЛКИНА, учитель математики школы №1 ст. Зеленчукской имени В.П.Леонова, лауреат конкурса «Учитель года России»-2018, Карачаево-Черкесская Республика










 Выбор читателей
Выбор читателей







Комментарии