ЕГЭ 2022. Профильный экзамен по математике станет сложнее – мнение эксперта

В 2020 году произошли существенные изменения в структуре контрольно-измерительных материалов ОГЭ по математике в 9‑м классе. Эти изменения были необходимы для того, чтобы привести экзаменационные задания в соответствие с действующими стандартами ФГОС. Прошло два года, и мы, учителя математики, с нетерпением ждали демонстрационной версии профильного экзамена по математике, чтобы оценить, насколько изменится структура экзаменационной работы в этом учебном году по сравнению с предыдущими. Ведь на протяжении большого количества лет структура КИМов профильного ЕГЭ по математике не менялась.

Изменения действительно произошли, и можно с уверенностью утверждать: профильный экзамен по математике станет сложнее, потому что из работы удалены первые самые легкие задания – задачи 1 и 2, проверяющие умение использовать приобретенные знания и умения в практической и повседневной жизни (уровень 5-6-х классов), и задание 3, проверяющее умение выполнять действия с геометрическими фигурами, координатами и векторами.

Чем же заменили эти задачи? Мы можем частично ответить на этот вопрос, опираясь на опубликованный демонстрационный вариант, но, согласитесь, одного варианта недостаточно, чтобы составить полное представление о разнообразии новых заданий. Именно поэтому очень важно иметь под рукой пособие, авторами которого являются специалисты, принимающие непосредственное участие в разработке заданий единого государственного экзамена по математике профильного уровня. Такими пособиями, в которых учтены все изменения ЕГЭ по математике, являются сборники издательства «Экзамен» под редакцией И.В.Ященко: «ЕГЭ 2022. Математика. Профильный уровень. 50 вариантов. Типовые варианты экзаменационных заданий от разработчиков ЕГЭ» и «ЕГЭ 2022. Математика. Профильный уровень. 37 вариантов. Типовые варианты экзаменационных заданий от разработчиков ЕГЭ».

Рассмотрим подробнее изменения в структуре КИМов 2022 года. Новыми являются задание 9, проверяющее умение выполнять действия с функциями, и задание 10 (повышенного уровня сложности), проверяющее умение моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий, при этом в первой части работы осталось задание базового уровня сложности, проверяющее те же самые умения. Понятно, что изменилась привычная для учителей математики нумерация заданий и их количество уменьшилось с 19 до 18. Изменения в системе оценивания коснулись второй части работы в заданиях с развернутым ответом. Так, стереометрическая задача 13 оценивается теперь в три первичных балла, экономическая задача 15 – в два балла, а максимальное общее количество баллов за экзаменационную работу снизилось до 31.

Обратимся к учебному пособию издательства «Экзамен», где представлено 50 тренировочных вариантов с учетом введенных изменений.

Анализируя представленные в сборнике варианты задания 9, проверяющего умение выполнять действия с функциями, можно сделать вывод о том, что для успешного их выполнения выпускник должен уметь от графического способа задания функции переходить к аналитическому. Приведем пример такого задания.

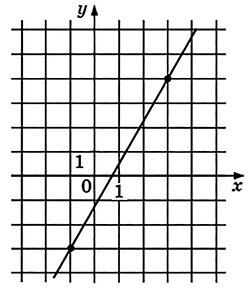
Вариант 1. Задание №9. На рисунке изображен график функции f(x)=kx+b. Найдите значение х, при котором выполнено f(x) = -13,5.

Понятно, что для выполнения подобных заданий школьникам необходимо вспомнить разделы курса алгебры 7-9-х классов, связанные с элементарными функциями и их графиками. Введение подобного задания в структуру КИМов ЕГЭ по математике мне кажется весьма целесообразным, так как на изучение этой темы выделяется большое количество часов, а в предыдущей версии КИМов профильного экзамена по математике в заданиях с кратким ответом умения выполнять действия с функциями не проверялись.

В новой версии экзаменационной работы в заданиях с кратким ответом содержится две задачи на тему «Элементы комбинаторики, статистики и теории вероятности». Предлагаю обратить внимание на примеры заданий 10 повышенного уровня сложности на эту тему из сборника «ЕГЭ 2022. Математика. Профильный уровень. 50 вариантов. Типовые варианты экзаменационных заданий от разработчиков ЕГЭ».

Вариант 11. Задание №10. Первый член последовательности целых чисел равен 0. Каждый следующий член последовательности с вероятностью р = 20/33  на единицу больше предыдущего и с вероятностью 1-р на единицу меньше предыдущего. Какова вероятность того, что какой-то член этой последовательности окажется равен -1?

Вариант 26. Задание №10. Первый игральный кубик обычный, а на гранях второго кубика нет чисел, больших, чем 2, а числа 1 и 2 встречаются по три раза. В остальном кубики одинаковые. Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпало 1 и 2 очка. Какова вероятность того, что бросали второй кубик?

Все описанное выше не входило в прототипы заданий профильного ЕГЭ прошлых лет и является абсолютно новым. Нельзя сказать, что оно будет легким для наших выпускников. Ведь для успешного решения этих задач необходимо внимательно ознакомиться с условием, составить правильную математическую модель и применить знания по нахождению вероятности события в конкретной ситуации. Таким образом, для успешной подготовки школьников к профильному экзамену учителям математики необходимо больше, чем раньше, уделять внимания задачам на тему «Элементы комбинаторики, статистики и теории вероятности».

Опубликован проект приказа, регламентирующего минимальное количество баллов ЕГЭ Общественное обсуждение инициативы Минпросвещения о минимальных баллах по результатам ЕГЭ в новом учебном году продлится до 16 сентября. Соответствующий документ устанавливает минимальный объем баллов Единого государственного экзамена, который выпускникам школ необходимо набрать для поступления в образовательные...

Образование UG.RU